The idea for this article came from a question on Stackoverflow. The question is about the possibility of writing the following authorization rule in ASP.NET Core:
C#
[Authorize(Roles = "Expert && (ReadWrite || ReadOnly)")]
This syntax is not supported by the Authorize attribute. It is still possible to achieve his ends by using the attribute 2 times:
C#
[Authorize(Roles = "Expert")]
[Authorize(Roles = "ReadWrite, ReadOnly")]
But it's not fun (and too simple). In this post, I will show you how to support the first syntax (and more) by writing a small parser for this language.
The goal is to "understand" the content of the string. It is therefore necessary to extract the different information: operators and names of roles while managing priorities (parentheses). The idea is to obtain a syntactic tree representing the expression:
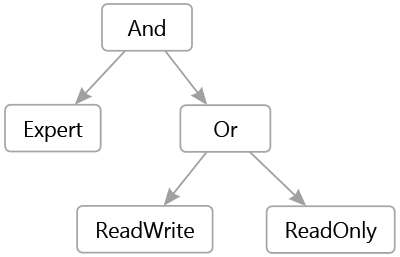
Before we get to that point, let's start with the basics. A language, without going into the theory, is:
- An alphabet: a set of valid characters
- Words: a coherent set of letters of the alphabet
- A grammar: a coherent set of words. For those interested, there are different types of grammar. Noam Chomsky, a great linguist, classified them into 4 categories, also known as the Chomsky hierarchy
To parse our language, we must begin by defining these 3 elements.
The alphabet is composed of:
- of letters
[a-zA-Z], - characters
&, |, ( and ), - and spaces.
There are 3 types of words:
- The operators:
&& and ||, - The parentheses
( and ), - Roles: set of letters
[a-zA-Z] +.
The context-free grammar is the following:
S:: = Expression
Expression:: = SubExpression
| SubExpression '&&' Expression
| SubExpression '||' Expression
SubExpression:: = '(' Expression ')'
| RoleName
RoleName:: = [a-zA-Z]
Let's take the example of the expression above to understand how it derives from grammar:
Expression
SubExpression && Expression
RoleName && SubExpression
'Expert' && (Expression)
'Expert' && (SubExpression || Expression)
...
'Expert' && ('ReadWrite' || 'ReadOnly')
#The code
The first step is to extract the tokens (the different words of the chain). We go through the string character by character and we store the tokens in a list:
C#
List<string> tokens = new List<string>();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < text.Length; i++)
{
char c = text[i];
switch (c)
{
case ' ':
if (sb.Length == 0)
continue;
sb.Append(c);
break;
case '(':
case ')':
if (sb.Length > 0)
{
tokens.Add(sb.ToString());
sb.Clear();
}
tokens.Add(c.ToString(CultureInfo.InvariantCulture));
break;
case '&':
case '|':
if (sb.Length != 0)
{
char prev = sb[sb.Length - 1];
if (c == prev) // && or ||
{
sb.Remove(sb.Length - 1, 1); // remove last char
tokens.Add(sb.ToString().Trim());
sb.Clear();
tokens.Add(c == '&' ? "&&" : "||");
break;
}
}
sb.Append(c);
break;
default:
sb.Append(c);
break;
}
}
if (sb.Length > 0)
{
tokens.Add(sb.ToString());
}
At the end we end up with a list of valid tokens, but we do not know if they have any meaning. We must now go through these tokens and check that it respects grammar. For this it is enough to transcribe the grammar in C#:
- 1 rule ⇒ 1 method
- 1 '|' or '&' ⇒ if / else if
C#
static Node Parse(string[] tokens)
{
int index = 0;
return ParseExp(tokens, ref index); // Rule 1
}
static Node ParseExp(string[] tokens, ref int index)
{
Node leftExp = ParseSubExp(tokens, ref index);
if (index >= tokens.Length) // last token => Rule 2
return leftExp;
string token = tokens[index];
if (token == "&&") // Rule 3
{
index++;
Node rightExp = ParseExp(tokens, ref index);
return new AndNode(leftExp, rightExp);
}
else if (token == "||") // Rule 4
{
index++;
Node rightExp = ParseExp(tokens, ref index);
return new OrNode(leftExp, rightExp);
}
else
{
throw new Exception("Expected '&&' or '||' or EOF");
}
}
static Node ParseSubExp(string[] tokens, ref int index)
{
string token = tokens[index];
if (token == "(") // Rule 5
{
index++;
Node node = ParseExp(tokens, ref index);
if (tokens[index] != ")")
throw new Exception("Expected ')'");
index++; // Skip ')'
return node;
}
else
{
index++;
return new RoleNode(token); // Rule 6
}
}
The code logically follows the grammar. We start with the entry point of the grammar, which calls the Expression rule that calls the rule SubExpression and, depending on the token, chooses the right rule…
In the end, we get a tree representing the original expression. So we can evaluate what was the goal. The full code, including the evaluator, is available on GitHub: https://gist.github.com/meziantou/10603804.
In 130 lines of code we can write a parser able to understand a Boolean expression (OR, AND, XOR, NOT, and priority). For those who want more:
- This is a LL parser. This type of parser is rather limited. For more complex needs there are others: LALR, LR, GLR.
- This parser could be improved, for example by "streaming" the tokens instead of extracting them all at the beginning. This makes it possible to process big expressions without deteriorating the performances.
- Writing a parser is fun once or twice for small grammars. Then you can look at tools such as ANTLR or Gold Parser whose purpose is to generate them for you.
The theory of languages is an exciting subject. Do not hesitate to take a look at the opportunity 😉
Do you have a question or a suggestion about this post? Contact me!